Determinar os prazos de amortização de um empréstimo, os montantes de pagamento periódico, o valor total de pagamentos,
ou as taxas de juro pode ser algo complexo. Para facilitar este tipo de cálculos, o GnuCash tem uma
Calculadora de amortização de empréstimos interna. Para aceder à calculadora, vá a → .
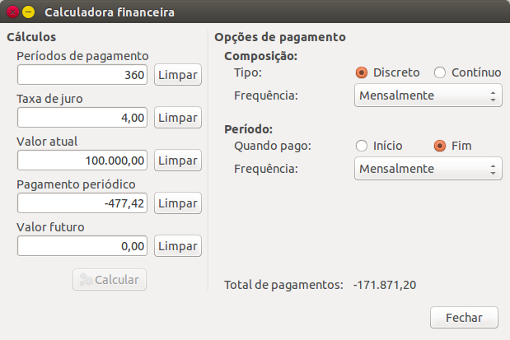
A calculadora de amortização de empréstimos do GnuCash.
A calculadora de amortização de empréstimos pode ser usada para calcular qualquer um dos parâmetros Períodos de pagamento, Taxa de juro, Valor atual, Pagamento periódico, ou Valor futuro, desde que os outros quatro estejam definidos. Também terá de especificar a composição e os métodos de pagamento.
Períodos de pagamento - o número de períodos de pagamento.
Taxa de juro - a taxa de juro nominal do empréstimo, i.e., a taxa de juro anual.
Valor presente - o valor presente do empréstimo, i.e., o valor atual em dívida.
Pagamento periódico - o montante a pagar por cada período.
Valor futuro - o valor futuro do empréstimo, i.e., o montante em dívida após todos os pagamentos terem terminado.
Composição - existem dois métodos de composição de juros, discreta e contínua. Para composição discreta, selecione a frequência de composição na lista, desde anualmente até diariamente.
Pagamentos - a lista permite-lhe selecionar a frequência de pagamento, desde anualmente até diariamente. Também pode selecionar se os seus pagamentos ocorrem no início ou no final do período. Pagamentos feitos no início do período de pagamento têm juros aplicados ao pagamento assim como qualquer dinheiro já pago ou ainda em dívida.
Qual é a sua prestação mensal num empréstimo de 100.000€ com a duração de 30 anos com uma taxa fixa de 4%, composta mensalmente?
Este cenário é mostrado na imagem exemplo acima. Para realizar este cálculo, defina os períodos de pagamento para 360 (12 meses x 30 anos), a taxa de juro para 4%, o valor presente para 100.000, deixe o pagamento periódico vazio e defina o valor futuro para 0 (não quer ficar a dever nada no final do empréstimo). A composição é mensal, os pagamentos são mensais e assuma que os pagamentos são feitos no final do período e que a composição é discreta. Agora, clique em ao fundo à esquerda. Deverá ver um pagamento periódico de -477.42€.
Resposta: tem de fazer pagamentos mensais de 477.42€.
Quanto tempo leva a pagar um empréstimo de 20.000€ à taxa de juro fixa de 10% composta mensalmente, se pagar 500€ por mês?
Para realizar este cálculo, deixe Períodos de pagamento vazio, defina Taxa de juro para 10, Valor atual para 20.000, Pagamento periódico para -500, e Valor futuro para 0 (não quer ficar a dever nada no final do empréstimo). A Composição é Mensalmente, os Pagamentos são Mensalmente, assuma pagamentos no Fim do Período e Composição Discreta. Agora, clique em . Deverá ver 49 no campo Períodos de pagamento.
Resposta: pagaria o empréstimo em 4 anos e 1 mês (49 meses).
Para podermos discutir as fórmulas matemáticas usadas pela calculadora de amortização de empréstimos, primeiro temos de definir algumas variáveis.
n == número de período de pagamentos
%i == taxa de juro nominal aplicada, TAN
VA == valor atual
PGT == pagamento periódico
VF == valor futuro
FC == frequência de composição por ano
FP == frequência de pagamento por ano
Valores normais para FC e FP são:
1 == anual
2 == semestral
3 == quadrimestral
4 == trimestral
6 == bimensal
12 == mensalmente
24 == quinzenalmente
26 == quinzenal
52 == semanalmente
360 == diariamente
365 == diariamente
Quando é requerida uma solução para n, VA, PGT ou VF, a taxa de juro nominal (i) tem primeiro de ser convertida em taxa de juro efetiva por período de pagamento (ief). Esta taxa, ief, é então usada para calcular a variável selecionada. Qunado é requerida uma solução para i, o cálculo produz a taxa de juro efetiva, ief. Logo, precisamos de funções para converter i em ief e ief em i.
Para converter de i em ieff,são usadas as seguintes expressões:
Juro discreto: ief = (1 + i/FC)^(FC/FP) - 1
Juro contínuo: ief = e^(i/FP) - 1 = exp(i/FP) - 1
Para converter ief em i, São usadas as seguintes expressões:
Juro discreto: i = FC*[(1+ief)^(FP/FP) - 1]
Juro contínuo: i = ln[(1+ief)^FP]
 | Nota |
|---|---|
NOTA: nas equações abaixo para a transação financeira, todas as taxas de juro são efetivas, “ief”. | |
Há uma equação que fundamentalmente, liga as cinco variáveis. É conhecida pela equação financeira básica:
VA*(1 + ief)^n + PGT*(1 + iefX)*[(1+ief)^n - 1]/ief + VF = 0
Onde: X = 0 para pagamentos no final do período e
X = 1 para pagamentos no início do período
A partir desta equação, podem ser derivadas funções resolvidas em ordem a cada variável individual. Para uma explicação
detalhada sobre a derivação desta equação, veja os comentários no ficheiro src/calculation/fin.c, no código fonte do
GnuCash. As variáveis A, B, e C são definidas primeiro, para tornar as equações posteriores mais simples
de ler.
A = (1 + ief)^n - 1
B = (1 + iefX)/ief
C = PGT*B
n = ln[(C - VF)/(C + VA)]/ln((1 + ief)
VA = -[VF + A*C]/(A + 1)
PGT = -[VF + VA*(A + 1)]/[A*B]
VF = -[VA + A*(VA + C)]
A solução para o juro é dividida em dois casos:
O caso mais simples para quando PGT == 0 dá a solução:
i = [VF/VA]^(1/n) - 1
O caso em que PGT != 0 é razoavelmente complexo e não será discutido aqui. Em vez de envolver uma função exatamente resolúvel, determinar a taxa de juro quando PMT !=0 envolve um processo interativo. Por favor, veja o ficheiro src/calculation/fin.para uma explicação detalhada.
Vamos recalcular o Secção 7.3.1, “Exemplo: pagamentos mensais”, desta vez usando as fórmulas matemáticas em vez da calculadora de amortização de empréstimos. Qual é o seu pagamento mensal num empréstimo de 100.000€ a 30 anos, com uma taxa fixa de 4%, composta mensalmente?
Primeiro vamos definir as variáveis: n = (30*12) = 360, VA =100000, PGT =desconhecido, VF = 0, i = 4%=4/100=0.04, FC = FP = 12, X = 0 (pagamentos no final do período).
O segundo passo é converter a taxa de juro nominal (i) para taxa de juro efetiva (ief). Uma vez que a taxa é composta mensalmente, discreta, usamos: ief = (1 + i/FC)^(FC/FP) - 1, que dá ief = (1 + 0.04/12)^(12/12) - 1, igual a ief = 1/300 = 0.0033333.
Agora podemos calcular A e B. A = (1 + ief)^n - 1 = (1 + 1/300)^360 - 1 = 2.313498. B = (1 + iefX)/ief = (1 + (1/300)*0)/(1/300) = 300.
Com A e B, podemos calcular PGT. PGT = -[VF + VA*(A + 1)]/[A*B] = -[0 + 100000*(2.313498 + 1)] / [2.313498 * 300] = -331349.8 / 694.0494 = -477.415296 = -477.42.
Resposta: tem de fazer pagamentos mensais de 477.42€.