ローン債務償還計画、定期返済額、総支払額、または利率に関して決定することは、少し複雑です。
GnuCashには、この種の計算を容易にするための、内蔵の財務計算機があります。
財務計算機にアクセスするためには、
→
を選択してください。
財務計算機は、支払期間、利率、現在価値、定期的支払額、将来価値のうち4つのパラメータを与えると、残りの一つを計算します。 複利計算方法と支払い方法も指定する必要があります。
支払期間 - 返済期間の回数です。
利率 - ローンの表面利率、すなわち実質年率です。
現在価値 - ローンの現在の価値、すなわち借りているローンの現在額です。
定期的支払額 - 単位期間あたりに支払う金額です。
将来価値 - ローンの将来の価値、すなわちすべての返済期間が終わった後に借りている金額です。
複利 - 離散と連続の2つの複利計算方法が存在しています。 離散複利計算の場合はポップアップメニューで離散的な複利計算の頻度を選択します。毎年から毎日までの変動幅があります。
期間 - ポップアップメニューで、毎年から毎日までの頻度のパターンから支払い頻度を選択します。 支払いが初日に発生するか、または末日に発生するかも選択します。 支払期間の初日に支払いを行う場合は、これまでに支払いを行った金額、またはまだ借りている金額と同じように利子が適用されます。
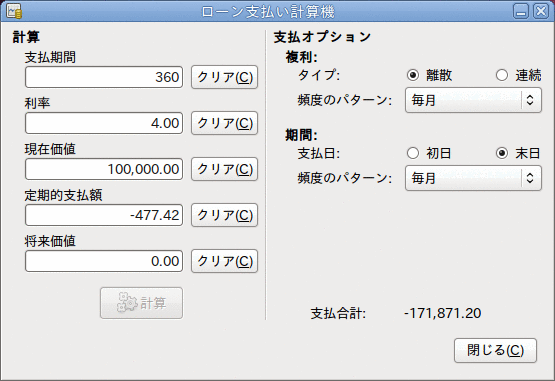
100,000ドルを30年間、4%の固定金利、毎月の複利計算で毎月払いにした時、毎月の支払額はいくらでしょうか?
この例のシナリオでの画像は前のようになります。 この計算を実行するために、支払期間に360(12カ月x30年間)を入力、利率に4を入力、現在価値に100000を入力、定期的支払額に何も入力しない、将来価値に0を入力します(ローンの終了のときに何も借りていません)。 複利の設定は離散、毎月にします。期間の設定は末日、毎月にします。 そして支払合計の横にあるボタンを押します。 定期的支払額に-477.42が表示されます。
答え: 毎月払い金額は477.42ドルになります。
20,000ドルのローンを返済するのに、10%の固定金利、毎月の複利計算、1カ月あたり500ドル支払うなら、どれくらいの期間がかかるでしょうか?
この計算を実行するためには、支払期間を空白にします。利率に10を入力します。現在価値に20000を入力します。定期支払額に-500を入力します。そして将来価値に0を入力します(ローンの終了のときに何も借りていません)。 複利の設定は離散、毎月にします。期間の設定は末日、毎月にします。 そして支払合計の横にあるボタンを押します。 支払期間に48が表示されます。
答え: 4年(48カ月)後にローンを完済します。
財務計算機で使用される数式を説明するためには、まず、いくつかの変数を定義しなければいけません。
n == 支払期間の数
%i == 表面利率、NAR
PV == 現在価値
PMT == 定期支払額
FV == 将来価値
CF == 1年あたりの複利計算の頻度
PF == 1年あたりの支払い頻度
CFとPFの標準の値はそれぞれ次の通りです。
1 == 毎年
2 == 年2回
3 == 年3回
4 == 四半期ごと
6 == 2カ月ごと
12 == 毎月
24 == 月2回
26 == 隔週
52 == 毎週
360 == 毎日(360)
365 == 毎日(365)
n、PV、PMTまたはFVを求める時には、最初に表面利率(i)を、支払いの期間あたりの実効利率(ieff)に変換しなければなりません。 このレート(ieff)は、後に選択された変数を計算するのに使用されます。 iを求める時には、計算によって実効利率(ieff)を求めます。 したがって、iからieffまで変換する機能とieffからiまで計算する機能が必要です。
iからieffまで変換するためには次の式を使用します。 離散的な利率: ieff = (1 + i/CF)^(CF/PF) - 1 連続的な利率: ieff = e^(i/PF) - 1 = exp(i/PF) - 1 ieffからiまで変換するためには次の式を使用します。 離散的な利率: i = CF*[(1+ieff)^(PF/CF) - 1] 連続的な利率: i = ln[(1+ieff)^PF]
 | 注記 |
|---|---|
以降で説明する、金融取引のための方程式では、すべての利率が実効利率「ieff」です。 簡潔にするために、文字では単に「i」と表記します。 | |
一つの方程式が基本的に5個すべての変数を関連付けます。 これは基本的な財務方程式として知られています。
PV*(1 + i)^n + PMT*(1 + iX)*[(1+i)^n - 1]/i + FV = 0
ここでXは次を表します。
X = 0 : 支払期間の終了時
X = 1 : 支払期間の開始時この方程式からそれぞれの変数を求める関数が導き出されます。
この式を求める方法の詳細についてはGnuCashソースコードのファイルsrc/calculation/fin.cにあるコメントを参照してください。
後の方程式を読むのをより簡単にするために、変数A、B、およびCを最初に定義します。
A = (1 + i)^n - 1 B = (1 + iX)/i C = PMT*B n = ln[(C - FV)/(C + PV)]/ln((1 + i) PV = -[FV + A*C]/(A + 1) PMT = -[FV + PV*(A + 1)]/[A*B] FV = -[PV + A*(PV + C)] 利率のための解は2つの場合に分かれます。 PMT===0 の場合は簡単で、解は次のようになります。 i = [FV/PV]^(1/n) - 1
PMT!=0の場合は非常に複雑であり、ここで記述することはできません。 PMT!=0の場合、正確に求めることができる関数があるのではなく、利率を決定するに反復演算が必要となります。 詳細な説明はsrc/calculation/fin.cソースファイルを参照してください。
「例: 毎月払い」を再計算してみましょう。今回は財務計算機ではなく数式を使用します。 100,000ドルを30年間、4%の固定金利、毎月の複利計算で毎月払いにした時、毎月の支払額はいくらでしょうか?
最初に変数を定義します。 n = (30*12) = 360 、 PV = 100000、 PMT = 未知、 FV = 0、 i = 4%=4/100=0.04、 CF = PF = 12、 X = 0 (支払期間の終了時)。
第2ステップでは、表面利率(i)を実効利率(ieff)に変換します。 利率は離散的な毎月複利のため、次のようになります。 ieff = (1 + i/CF)^(CF/PF) - 1 = (1 + 0.04/12)^(12/12) - 1 = 1/300 = 0.0033333。
次は、AとBを計算します。 A = (1 + i)^n - 1 = (1 + 1/300)^360 - 1 = 2.313498。 B = (1 + iX)/i = (1 + (1/300)*0)/(1/300) = 300。
AとBを使って、PMTを計算します。 PMT = -[FV + PV*(A + 1)]/[A*B] = -[0 + 100000*(2.313498 + 1)] / [2.313498 * 300] = -331349.8 / 694.0494 = -477.415296 = -477.42。
答え: 毎月払い金額は477.42ドルになります。