确定分期贷款还款计划、每期还款金额、总还款额或利率可能并不容易。GnuCash内置的贷款还款计算器可以帮助你方便地进行这些计算。通过
→ 打开。
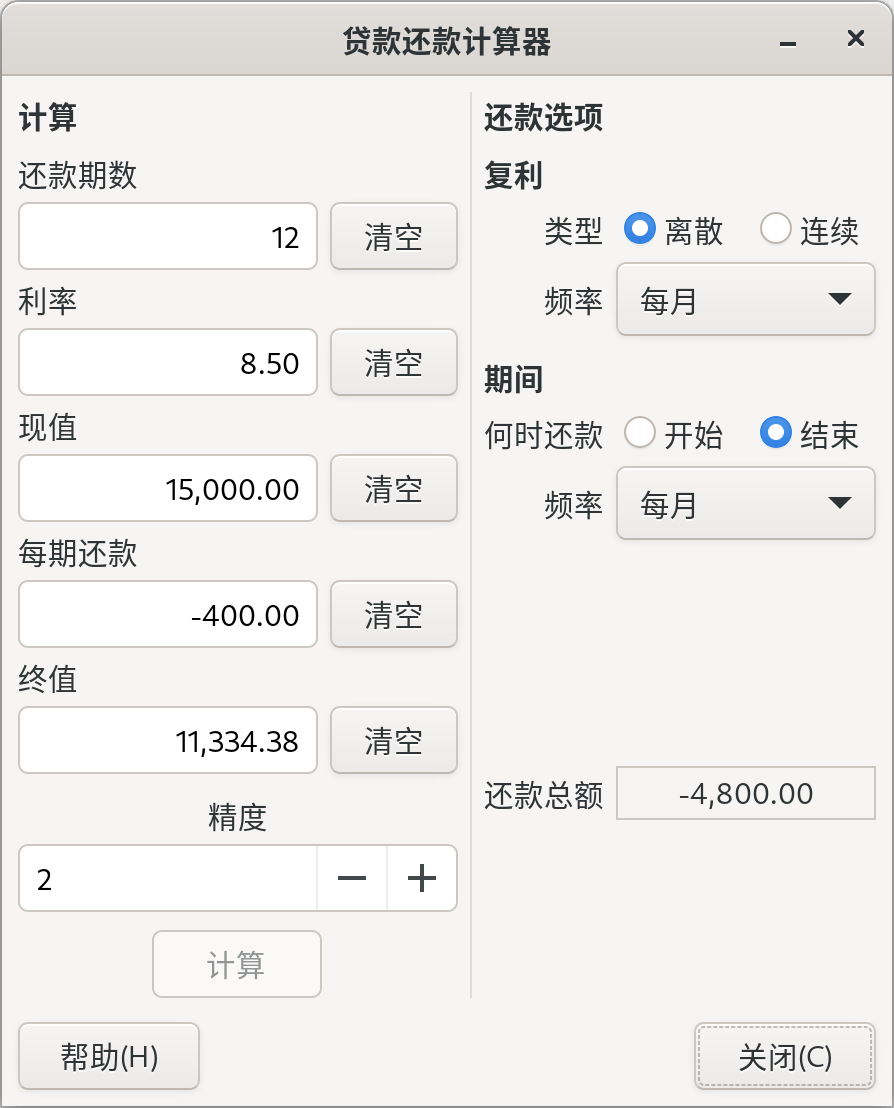
贷款还款计算器能够计算的数值有还款期数、利率、现值, 每期还款金额和终值,只要给出其它四项数值就可以计算任一数值。另外还要指定复利方案和还款方案。
- 还款期数
要支付多少次还款。
- 利率
贷款的名义利率(NAR),也就是常说的年利率。
- 现值
贷款当前的价值,也就是当前欠款金额。
- 每期还款
每期要偿还的金额。
- 终值
贷款将来的价值,也就是全部还款期结束后剩余的欠款金额。
- 复利
有两种复利计算方法,离散复利和连续复利。选择离散复利时,要从下拉框中指定从每年到每天不等的复利频率。
- 还款
通过下拉框选择还款频率,每年到每天不等。也可以选择在期初还是在期末时还款。如果选择期初还款,还款额会同当前欠款金额一起计算利息。
一份总计100,000元、时长30年、固定利率4%、复利计息的贷款,其月还款额是多少呢?
这一分期方案如下图所示。要执行计算,将还款期数设为360(12个月×30年),利率为4,现值为100000,每期还款金额留空,终值设为0(你不想在还款结束后仍欠款)。复利是每月,还款是每月,另假设期末还款、离散复利。现在点击按钮,可见结果为-477.42。
答案:每月需还款477.42元。
一份20,000元、10%固定利率、按月复利的贷款,每月还款500元,要多久才能偿清?
要执行计算,还款期数留空,设置利率为10、现值为20000、每期还款金额为-500、终值为0(你不想在还款结束后仍欠款)。复利为每月、还款为每月,假设期末还款、离散复利。现在点击按钮,可见还款期数处显示49。
答案:用4年零1个月内偿清贷款(49个月)。
在讨论贷款还款计算器所使用的数学公式之前,先定义一些变量。
n == 还款期数 %i == 收取的名义利率 PV == 现值 PMT == 每期还款金额 FV == 终值 CF == 每年计息频率 PF == 每年还款频率 每年计息频率(CF)和每年还款频率(PF)一般为: 1 == 每年 2 == 每半年 3 == 每三分之一年 4 == 每季度 6 == 每两个月 12 == 每月 24 == 每半月 26 == 每两周 52 == 每周 360 == 每天 365 == 每天
要求解 n、PV、PMT或FV,先要将名义利率(i)转换为还款期时长的有效利率(ieff)。这一利率(ieff)随后用于计算需要求解的变量。需要求解i时,计算结果是有效利率(ieff)。因此,需要将i转换为ieff,也要将ieff转换为i。
将i转换为ieff,使用公式: 离散复利:ieff = (1 + i/CF)^(CF/PF) - 1 连续复利:ieff = e^(i/PF) - 1 = exp(i/PF) - 1 将ieff转换为i,使用公式: 离散复利:i = CF*[(1+ieff)^(PF/CF) - 1] 连续复利:i = ln[(1+ieff)^PF]
 | 注意 |
|---|---|
在下文处理金融业务的公式中,所有利率均指有效利率“ieff”。出于简洁考虑,此符号缩写为“i”. | |
一个方程可将所有这五个变量联系起来,这也就是常说的基本金融方程:
PV*(1 + i)^n + PMT*(1 + iX)*[(1+i)^n - 1]/i + FV = 0
其中: X = 0 表示期末还款, and
X = 1 表示期初还款由此方程可推导出计算各独立变量的函数表达式。有关方程推导的详细解释,参见GnuCash源代码文件
libgnucash/app-utils/calculation/fin.c
中的注释。首先定义A、B、C三个变量,以使后面给出的公式更易读。
A = (1 + i)^n - 1 B = (1 + iX)/i C = PMT*B n = ln[(C - FV)/(C + PV)]/ln((1 + i) PV = -[FV + A*C]/(A + 1) PMT = -[FV + PV*(A + 1)]/[A*B] FV = -[PV + A*(PV + C)] 求解利率分为两种情况。 简单情况为 PMT == 0 时,相应解为: i = [FV/PV]^(1/n) - 1
PMT != 0的情况相当复杂,这里不会列出。。当在PMT != 0的情况下求解利率时,无法给出准确的可解函数,相关计算需涉及迭代过程。详细说明请参见libgnucash/app-utils/calculation/fin.c源文件。
现在重新计算第 8.3.1 节 “示例:每月还款”,这次我们使用数学公式而非贷款还款计算器。对于一笔为期30年、固定利率4%、复利计息、总计100,000元的贷款,你每个月要还多少钱呢?
首先,定义变量 n = (30*12) = 360, PV = 100000, PMT = 未知, FV = 0, i = 4%=4/100=0.04, CF = PF = 12, X = 0 (所有还款期结束)
第二步,将名义利率(i)转换为有效利率(ieff)。由于利率是按月复利,而且是离散的,使用: ieff = (1 + i/CF)^(CF/PF) - 1 , 其中 ieff = (1 + 0.04/12)^(12/12) - 1 ,因此 ieff = 1/300 = 0.0033333。
现在我们可以计算A和B了。 A = (1 + i)^n - 1 = (1 + 1/300)^360 - 1 = 2.313498。 B = (1 + iX)/i = (1 + (1/300)*0)/(1/300) = 300。
算出A和B,可以计算 PMT。 PMT = -[FV + PV*(A + 1)]/[A*B] = -[0 + 100000*(2.313498 + 1)] / [2.313498 * 300] = -331349.8 / 694.0494 = -477.415296 = -477.42。
答案:你每月须还款477.42元。